An Ideal Jigsaw With Two Solutions

Sometimes you don't need a computer

Matt Parker asks for an 'ideal’ jigsaw with two solutions:

The criteria seem to be that the jigsaw should be (a) 25 pieces in a 5x5 grid (b) each edge type occurs exactly twice (c) there are exactly two solutions (d) in the two different solutions the maximum number of pieces are reoriented upside down. He’s done a search using a computer but that turns out to be unnecessary.

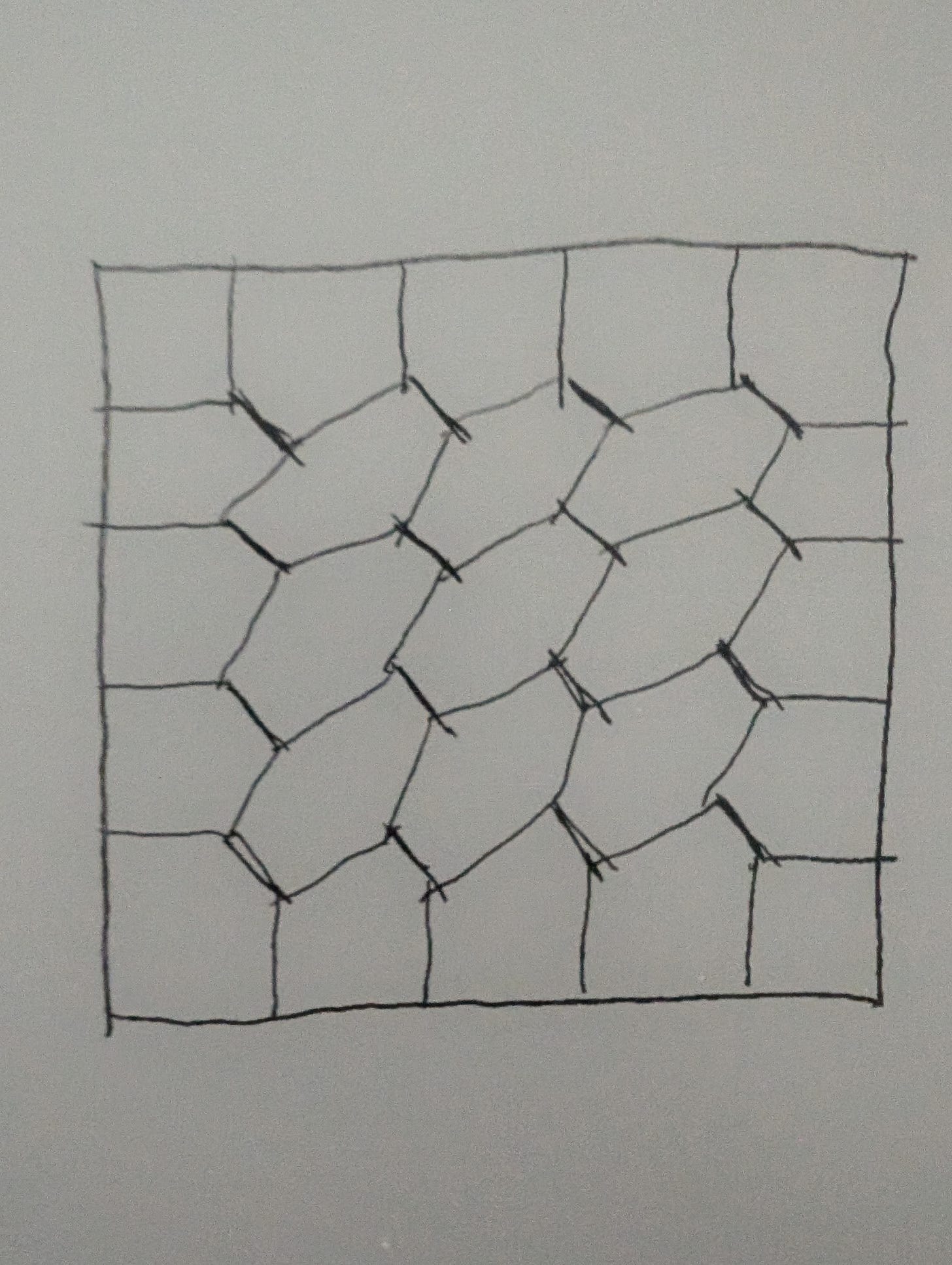
There’s a very simple mathematical trick which can be applied here. If the rows and columns are numbered 1-5, first swap columns 2 and 4, then swap rows 2 and 4, like this:

Then you flip it all upside down, and presto, all the criteria satisfied perfectly. Except… not quite. The problem is that this doesn’t result in two solutions, it results in four. You can independently decide whether to swap the rows and the columns. The most elegant fix for this seems to be to change the shapes of the pieces a bit so that instead of each piece just sharing an edge with the ones in the left, right, up, and down directions they also share with the ones in the upper right and lower left. This not only enforces that there are exactly two solutions, it also preserves the property that each edge type occurs exactly twice, even on the diagonal edges