Activation Functions
Commentary on existing ones and a suggestion of a possibly better one
I keep posting about the importance of functions inside of deep neural networks being sublinear but haven’t given an exact definition of that before. It’s sublinearity in the computer science asymptotic sense. The Taylor expansion should not only have a linear bound but either going to zero or at least have the positive and negative directions go to different asymptotics. If the function is defined by different formulas in different sections that criterion should apply to all of them.1
With that out the the way here’s how common activation functions look with a new suggestion at the bottom.
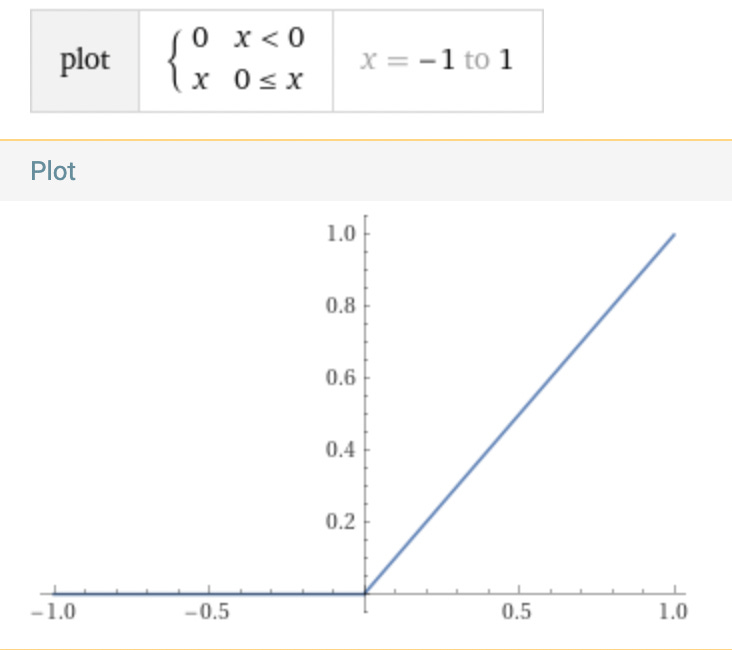
This is as nonlinear as you can get a monotonic function sublinear function to be and is trivial to compute. The one big problem is that it has that kink at 0. Is it too much to ask for a function to be continuously differentiable?
It’s okay to have insecurities about some areas being completely occluded and hence stop responding to training but if it’s that much of a problem for you you don’t have what it takes to work with DNNs and should go back to playing with linear functions.
GELU
We get it, you got rid of that kink, but the requirements specified a function which is monotonic, can you not read? Also maybe don’t use functions which are so obscure that I can’t figure out how to enter them into Wolfram Alpha.
Thank you for you following the requirements and there’s some argument to using Softmax here since you’re probably using it elsewhere anyway. But it does seem to take a large area to smooth that kink out and never quite gets to exactly RELU in either direction.
RELU with Sinusoidal Smoothing (RELUSS)
This is my new idea. Not only is the kink completely smoothed out, it’s done with a simple quick to calculate function which meets the requirements and reverts completely to RELU outside of that area.
Don’t ask about x*sin(x)